1、算法

1.1 二分搜索

binary search

有序数组，查一个数的角标。

public void halfSearch(int[] nums,int target)
&#123;
    int l = 0;
    int r = nums.length - 1;
    while( l <= r )
    &#123;
        int mid = (l+r)/2;
        if( target == nums[mid]) return mid;
        else if( target < nums[mid] ) r = mid - 1;
        else if( target > nums[mid] ) l = mid + 1;
    &#125;
    return -1;
&#125;

1.2 分治

1.3 排序

冒泡排序： 最好O（n），最差O（n2），平均O（n2）

public static void bubbleSort(int[] nums)
&#123;
    for(int i=0;i<nums.length;i++)
        for(int j=0;j<nums.length-1-i;j++)
            if(nums[j]>nums[j+1])
            &#123;
                int temp = nums[j];
                nums[j] = nums[j+1];
                nums[j+1] = temp;
            &#125;
&#125;

选择排序： 一直都是O（n2），最稳定的算法之一

public static void selectSort(int[] nums)
&#123;
    for(int i=0;i<nums.length - 1;i++)
    &#123;
        int minIndex = i;
        for(int j=i;j<nums.length;j++)
            if(nums[j]<nums[minIndex]) minIndex = j;
        int temp = nums[minIndex];
        nums[minIndex] = nums[i];
        nums[i] = temp;
    &#125;
&#125;

图的遍历

深度DFS配栈，广度BFS配队列

有项无环图

AOV，AOE

任务间有依赖关系，让你建任务表，就是拓扑排序

动态路径规划

Q1/A：有N*M个格子，从左上到右下，每个格子有数值，只能右，下，右下的走，怎么走总数最小？

构造二维数组dp，填入第一行，第一列
填入所有的数据

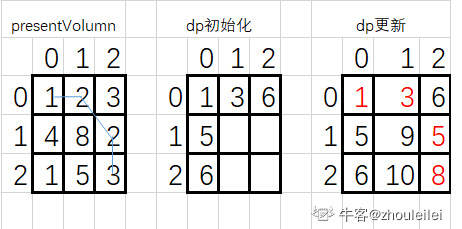
public int selectPresent(int[][] presentNum)
    &#123;
        if(presentNum.length == 0) return 0;
        if(presentNum[0].length == 0) return 0;

        int[][] dp = new int[presentNum.length][presentNum[0].length];
        dp[0][0] = presentNum[0][0];

        //初始化第0行
        for(int i=1;i<presentNum[0].length;i++)
            dp[0][i] = presentNum[0][i]+dp[0][i-1];

        //初始化第0列
        for(int i=1;i<presentNum.length;i++)
            dp[i][0] = presentNum[i][0]+dp[i-1][0];

        //循环dp，填入数据
        for(int i=1;i<presentNum.length;i++)
            for(int j=1;j<presentNum[0].length;i++)
                dp[i][j] = getMin(dp[i-1][j],dp[i][j-1], dp[i-1][j-1])+presentNum[i][j];

        return dp[presentNum.length-1][presentNum[0].length-1];
    &#125;
    private static int getMin(int a,int b,int c)
    &#123;
        if(a<=b && a<=c) return a;
        else if(b<=a && b<=c) return b;
        else if(c<=a && c<=b) return c;
        return -1;
    &#125;

Q2/A:

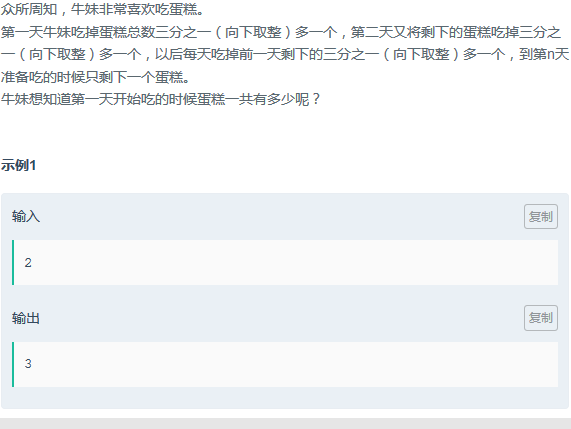
因为最后一天的面包数一定是1，根据1推出前面的面包数。

public int cakeNumber (int n) &#123;
        int[] dp = new int[n];
        dp[0] = 1;
        for(int i=1;i<dp.length;i++)
        &#123;
            dp[i] = ((dp[i-1]+1)*3)/2;
        &#125;

        return dp[n-1];
    &#125;

Q3/A:

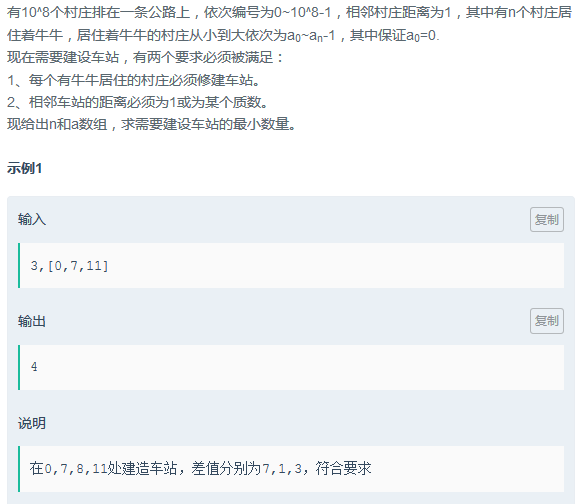
哥德巴赫猜想：

可以理解为将一个非质数表示为最少的质数和，分情况讨论：

1、当该非质数为偶数时，可以表示为两个质数的和（根据哥德巴赫猜想）；

2、当该非质数为奇数时，分解为p=(p-2)+2：

若p-2为质数，则可表示为两个质数的和

若p-2为非质数，则可表示为三个质数的和

 public int work (int n, int[] a) 
     &#123;
         int count = n;
         int length = 0;
         for(int i=1;i<a.length;i++)
         &#123;
             length  = a[i] - a[i-1];
             if(length == 1)
                 continue;
             else if(judge(length))
                 continue;
             else if(length%2 == 0)
             &#123;
                 count++;
                 continue;
             &#125;
             if(judge(length-2))
                 count++;
             else &#123;
                 count+=2;
             &#125;

         &#125;

         return count;
     &#125;

     private static boolean judge(int num)
     &#123;
         for(int i=2;i<num;i++)
             if(num%i==0)
                 return false;
         return true;
     &#125;
&#125;